Decompression Model

Introduction

The DecoTengu implements Buhlmann decompression model ZH-L16 with gradient factors by Erik Baker, which we will refer to as ZH-L16-GF.

The initial version of the Buhlmann decompression model (ZH-L16A) was found not safe enough, its parameters were revised and two new, more conservative versions were developed - ZH-L16B and ZH-L16C. Adding gradient factors, DecoTengu supports two decompression models

ZH-L16B-GF

used for dive table calculations

ZH-L16C-GF

used for real-time dive computer calculations

Parameters

The Buhlmann decompression model describes human body as 16 tissue compartments. For an inert gas and for each compartment the model assigns the following parameters

A

Buhlmann coefficient A.

B

Buhlmann coefficient B.

half life

Half-life time constant for inert gas, i.e. nitrogen, helium.

The gradient factors extension defines two parameters expressed as percentage

gf low

Controls how deep first decompression stop should start. The smaller value, the deeper first decompression stop.

gf high

Controls the time of decompression stops. The higher value, the shorter decompression time.

Equations

The parameters mentioned in previous section are used by two equations

1. Schreiner equation to calculate inert gas pressure in a tissue compartment.

2. Buhlmann equation extended with gradient factors by Erik Baker to calculate ascent ceiling in a tissue compartment.

Schreiner Equation

The Schreiner equation is

\[P = P_{alv} + R * (t - 1 / k) - (P_{alv} - P_{i} - R / k) * e^{-k * t}\]

Pressure \(P_{i}\) is initial pressure of inert gas in tissue compartment, i.e. pressure of nitrogen in human body at the surface. The result of the equation is pressure \(P\) in tissue compartment after time of exposure \(t\). The inert gas pressure value is fed recursively to the equation from start till end of a dive, this is \(P_{i} = P\) after each dive step lasting \(t\) minutes.

The variables of the equation are

\(P_{i}\)

Initial inert gas pressure in a tissue compartment.

\(P_{alv}\)

Pressure of inspired inert gas: \(P_{alv} = F_{gas} * (P_{abs} - P_{wvp})\)

\(t\)

Time of exposure in minutes.

\(k\)

Gas decay constant for a tissue compartment: \(k = ln(2) / T_{hl}\)

\(R\)

Rate of change of inert gas pressure: \(R = F_{gas} * P_{rate}\)

where

\(P_{abs}\)

Absolute pressure of current depth [bar].

\(F_{gas}\)

Inert gas fraction, i.e. 0.79 for air.

\(P_{rate}\)

Pressure rate change [bar/min] (for example, about 1 bar/min is 10m/min).

\(T_{hl}\)

Inert gas half-life time for tissue compartment.

\(P_{wvp}\)

Water vapour pressure.

The values for \(P_{rate}\) parameter can be

zero

constant depth exposure

negative

ascent during a dive

positive

descent during a dive

Example

Below, calculation of inert gas pressure in tissue compartment using Schreiner equation is performed. It is done for first compartment in ZH-L16B-GF decompression model and for dive profile described below when using EAN32

• descent from 0m to 30m at rate 20m/min

• dive at 30m for 20min

• ascent from 30m to 10m at rate 10m/min

For the example, the following assumptions are made

• surface pressure is 1 bar

• change of 10m depth is change of 1 bar pressure

• the water vapour pressure is 0.0627

For the start of a dive and descent from 0m to 30m the Schreiner equation variables are

\(P_{i} = 0.7902 * (1 - 0.0627) = 0.74065446\) (initial pressure of nitrogen in tissue compartment at the surface)

\(P_{abs} = 1\) (starting from 0m or 1 bar)

\(F_{gas} = 0.68\) (EAN32)

\(P_{alv} = 0.68 * (1 - 0.0627) = 0.637364\)

\(R = 0.68 * 2\) (20m/min is 2 bar per minute pressure change)

\(T_{hl} = 5.0\) (\(N_2\) half-life time for first tissue compartment in ZH-L16B-GF)

\(t = 1.5\) (1.5 minute to descent by 30m at 20m/min)

\(k = ln(2) / T_{hl} = 0.138629\)

and pressure in the first tissue compartment is

\[P = P_{alv} + 1.36 * (1.5 - 1 / k) - (P_{alv} - 0.74065446 - 1.36 / k) * e^{-k * 1.5} = 0.919397\]

Next, continue dive at 30m for 20 minutes

\(P_{i} = 0.919397\) (inert gas pressure in tissue compartment after descent to 30m)

\(P_{abs} = 4\) (30m or 4 bar)

\(P_{alv} = 0.68 * (4 - 0.0627) = 2.677364\)

\(R = 0.68 * 0\) (constant depth, no pressure change)

\(t = 20\)

and pressure in first tissue compartment is (note \(R\) is zero and cancels parts of equation)

\[P = P_{alv} + 0 - (P_{alv} - 0.919397 - 0) * e^{-k * 20} = 2.567490\]

Finally, ascent from 30m to 10m

\(P_{i} = 2.567490\)

\(R = 0.68 * (-1)\) (10m/min is 1 bar per minute pressure change, negative as it is ascent)

\(t = 2\) (2 minutes to ascend from 30m to 10m at 10m/min)

and pressure in first tissue compartment is

\[P = P_{alv} + (-0.68) * (2 - 1 / k) - (P_{alv} - 2.567490 - (-0.68) / k) * e^{-k * 2} = 2.421840\]

With DecoTengu, we can calculate pressure of nitrogen in the first tissue compartment for above dive profile using ZH_L16B_GF class

>>> from decotengu.engine import GasMix
>>> model = ZH_L16B_GF()
>>> ean32 = GasMix(0, 32, 68, 0)
>>> data = model.init(1)
>>> data = model.load(1, 1.5, ean32, 2, data)
>>> round(data.tissues[0][0], 6)
0.919397
>>> data = model.load(4, 20, ean32, 0, data)
>>> round(data.tissues[0][0], 6)
2.567491
>>> data  = model.load(4, 2, ean32, -1, data)
>>> round(data.tissues[0][0], 6)
2.42184

The relationship between dive time, absolute pressure of dive depth and inert gas pressure in a tissue compartment is visualized on figure Inert gas pressure in tissue compartment for a dive profile.

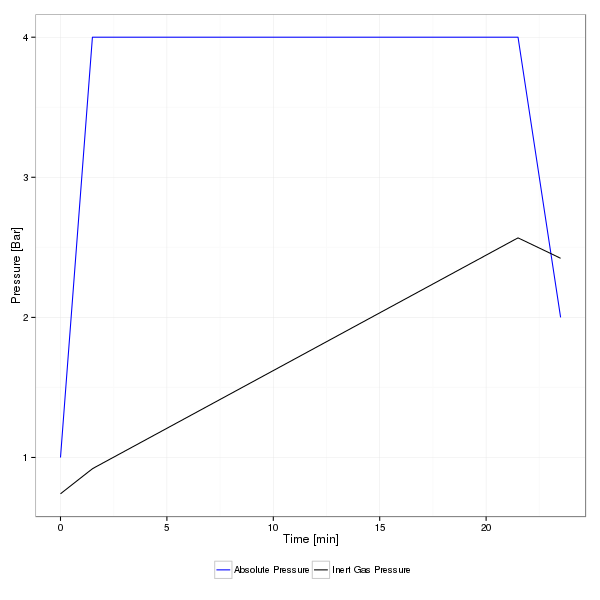
Inert gas pressure in tissue compartment for a dive profile

Buhlmann Equation

Buhlmann equation extended with gradient factors by Erik Baker is

\[P_l = (P - A * gf) / (gf / B + 1.0 - gf)\]

Tissue absolute pressure limit \(P_l\) determines depth of ascent ceiling, which is calculated using inert gas pressure \(P\) in tissue compartment (result of Schreiner equation), Buhlmann coefficients \(A\) and \(B\) (for given tissue) and current gradient factor value \(gf\).

Current gradient factor is a value, which changes evenly between values of gf low and gf high decompression model parameters. It has gf low value at first decompression stop and gf high value at the surface.

To support multiple inert gases, i.e. trimix with nitrogen and helium, we need to track pressure of each inert gas separately. The Buhlmann equation variables can be supported then with the following equations

\[ \begin{align}\begin{aligned}P = P_{n2} + P_{he}\\A = (A_{n2} * P_{n2} + A_{he} * P_{he}) / P\\B = (B_{n2} * P_{n2} + B_{he} * P_{he}) / P\end{aligned}\end{align} \]

where

\(P_{n2}\)

Pressure of nitrogen in current tissue compartment.

\(P_{he}\)

Pressure of helium in current tissue compartment.

\(A_{n2}\)

Buhlmann coefficient \(A\) for nitrogen.

\(B_{n2}\)

Buhlmann coefficient \(B\) for nitrogen.

\(A_{he}\)

Buhlmann coefficient \(A\) for helium.

\(B_{he}\)

Buhlmann coefficient \(B\) for helium.

Example

We continue the example described in Schreiner equation section. In the example, the nitrogen pressure in first tissue compartment at various depths is

Depth [m]	Runtime [min]	P [bar]
0	0	0.74065446
30	1.5	0.919397
30	21.5	2.567490
10	23.5	2.421840

The Buhlmann coefficients for the first tissue compartment in ZH-L16B-GF model are (nitrox dive, therefore we skip trimix extension)

\[ \begin{align}\begin{aligned}A = 1.1696\\B = 0.5578\end{aligned}\end{align} \]

We attempt to ascend to first decompression stop and use \(0.3\) as current gradient factor value

\[ \begin{align}\begin{aligned}(0.74065446 - 1.1696 * 0.3) / (0.3 / 0.5578 + 1.0 - 0.3) = 0.314886\\(0.919397 - 1.1696 * 0.3) / (0.3 / 0.5578 + 1.0 - 0.3) = 0.4592862\\(2.567490 - 1.1696 * 0.3) / (0.3 / 0.5578 + 1.0 - 0.3) = 1.7907266\\(2.421840 - 1.1696 * 0.3) / (0.3 / 0.5578 + 1.0 - 0.3) = 1.6730607\end{aligned}\end{align} \]

Using eq_gf_limit() function (we omit helium parameters by substituting them with 0 as the example uses nitrox gas mix only)

>>> eq_gf_limit(0.3, 0.74065446, 0, 1.1696, 0.5578, 0, 0)
0.31488600902007363
>>> eq_gf_limit(0.3, 0.919397, 0, 1.1696, 0.5578, 0, 0)
0.459286247718912
>>> eq_gf_limit(0.3, 2.567490, 0, 1.1696, 0.5578, 0, 0)
1.790726556208904
>>> eq_gf_limit(0.3, 2.421840, 0, 1.1696, 0.5578, 0, 0)
1.6730606957680387

Let’s put the calculations into the table

Depth [m]	Runtime [min]	P [bar]	Limit [bar]	Note
0	0	0.74065446	0.314886
30	1.5	0.919397	0.4592862
30	21.5	2.567490	1.7907266	~8m
10	23.5	2.421840	1.6730607	~7m

When starting ascent from 30 meters, the ceiling limit is at about 8m. After ascent to 10m, the ceiling limit changes to about 7m - the first (and any other) tissue compartment desaturates during ascent. This suggests, that to find exact depth of first decompression stop an algorithm will be required (see Algorithms section).

Calculations

The main code for decompression model is implemented in ZH_L16_GF class.

Inert gas pressure of each tissue compartment for descent, ascent and at constant depth is calculated by the ZH_L16_GF.load() method, which uses Schreiner equation.

The pressure of ascent ceiling of a diver is calculated with the ZH_L16_GF.ceiling_limit() method. The method allows to determine

• depth of first decompression stop - a diver cannot ascent from the bottom shallower than ascent ceiling

• length of decompression stop - a diver cannot ascent from decompression stop until depth of ascent ceiling decreases

References

• Baker, Erik. Understanding M-values.

• Baker, Erik. Clearing Up The Confusion About "Deep Stops".

• Baker, Erik. Untitled, known as "Deco Lessons".

• Powell, Mark. Deco for Divers, United Kingdom, 2010.

• HeinrichsWeikamp. OSTC dive computer source code.